اللجنة الجهوية لمراجعة البرامج والمناهج

إن التركيز في مادة الرياضيات و إيجاد طرق مختلفة لسؤال واحد، لهو غاية معظم ممارسي الرياضيات، إليكم بعض الطرق لحل بعض المسائل في انتظار إضافة طرق أخرى، أو حلول لمسائل أخرى:

- للبرهان أن ثلاث نقط مستقيمية
- للبرهان على توازي مستقيمين 
- للبرهان على تعامد مستقيمين
- للبرهان على منتصف القطعة
- لبرهان على تقايس قطعتين
- للبرهان أن رباعي متوازي الأضلاع
- للبرهان أن مثلث قائم الزاوية

للبرهان أن ثلاث نقط مستقيمية

1- التعريف: كل ثلاث نقط أو أكثر تنتمي إلى نفس المستقيم فهي نقط مستقيمية.	الأولى إعدادي
2- استعمال الزاوية المسقيمية: إذا كانت BÔA = 180° فإن: النقط A و B و O نقط مستقيمية.	الأولى إعدادي
3- استعمال منتصف قطعة: إذا كانت I منتصف القطعة [AB] فإن: النقط A و B و I نقط مستقيمية.	الأولى إعدادي
4- استعمال المسافات: إذا كانت AB + AC = BC فإن: النقطة A تنتمي إلى القطعة [BC] و منه: النقط A و B و C نقط مستقيمية.	الأولى إعدادي
5- استعمال تطابق المستقيمات: إذا كان (AC) يوازي (AB) فإن: (AC) و (AB) متطابقان و منه: النقط A و B و C نقط مستقيمية.	الأولى إعدادي
6- باستعمال التعامد: إذا كان (AC) و (AB) عموديان على نفس المستقيم . فإن: (AC) و (AB) متطابقان و منه: النقط A و B و C نقط مستقيمية.	الأولى إعدادي
7- باستعمال التوازي: إذا كان (AC) و (AB) متوازيان مع نفس المستقيم . فإن: (AC) و (AB) متطابقان و منه: النقط A و B و C نقط مستقيمية.	الأولى إعدادي
8- المتجهات: A و B و C نقط في المستوى إذا وجد عدد حقيقي k ، بحيث فإن: النقط A و B و C نقط مستقيمية. ملاحظة: هذه النتيجة يمكن البرهان عنها بطريقتين، إحداثيات نقطة أو علاقة شال.	الثالثة إعدادي
10- صور نقط مستقيمية بإزاحة أو تماثل محوري أو مركزي هي نقط مستقيمية. لأن الإزاحة و التماثل المحوري و التماثل المركزي يحافظون على استقامية النقط.	الثالثة إعدادي
11- إذا كانت y = mx + p معادلة المستقيم (AB)، حيث m و p عددان حقيقيان و M أفصولها a و أرتوبها b . و b = ma +p . فإن النقط A و B و M نقط مستقيمية.	الثالثة إعدادي

للبرهان على توازي مستقيمين

التعريف: المستقيمان المتوازيان، هما مستقيمان، إما متطابقان أو لا يشتركان في أية نقطة.	الأولى إعدادي
طريقة 1: إذا كان مستقيمان متعامدان، فكل مستقيم عمودي على أحدهما يكون موازيا للآخر.	الأولى إعدادي
طريقة 2: إذا كان مستقيمان متوازيان فكل مستقيم موازي لأحدهما يكون موازيا للآخر.	الأولى إعدادي
طريقة 3: صورة مستقيم بتماثل مركزي هو مستقيم يوازيه.	الأولى إعدادي
طريقة 4: إذا حدد لنا مستقيمان (D) و (L) مع قاطع لهما، زاويتان متناظرتان متقايستان فإن: (D) و (L) متوازيان.	الأولى إعدادي
طريقة 5: إذا حدد لنا مستقيمان (D) و (L) مع قاطع لهما، زاويتان متبادلتان ذاخليا متقايستان فإن: (D) و (L) متوازيان.	الأولى إعدادي
طريقة 6: إذا حدد لنا مستقيمان (D) و (L) مع قاطع لهما، زاويتان ذاخليتان من نفس الجهة متكاملتان فإن: (D) و (L) متوازيان.	الأولى إعدادي
طريقة 7: إذا كان المستقيمان (D) و (L) حاملي ضلعين متقابلين في متوازي الأضلاع فإن: (D) و (L) متوازيان.	الأولى إعدادي
طريقة 8: في مثلث ABC إذا كانت: I منتصف القطعة [AB] و: J منتصف القطعة [AC] فإن: (IJ) و (BC) مستقيمان متوازيان.	الثانية إعدادي
طريقة 9: صورة مستقيم بإزاحة هو مستقيم يوازيه.	الثانية إعدادي
طريقة 10: صورة مستقيمان متوازيان بتماثل محوري هما مستقيمان متوازيان، لأن التماثل المحوري يحافظ على توازي المستقيمات.	الثانية إعدادي
طريقة 11: (مبرهنة طاليس العكسية) في مثلث ABC إذا كانت: I نقطة من المستقيم (AB) و: J نقطة من المستقيم (AC) و: و: النقط A و B و I و النقط A و C و J في نفس الترتيب. فإن: (IJ) و (BC) مستقيمان متوازيان.	الثالثة إعدادي
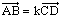
طريقة 12: إذا كانت: فإن: المستقيمان (AB) و (DC) متوازيان.	الثالثة إعدادي
طريقة 13: إذا كانت : (d) معادلته y = mx + p و المستقيم ('d) معادلته y = ax + b . و m = a . فإن المستقيمان (d) و ('d) متوازيان.	الثالثة إعدادي

للبرهان على تعامد مستقيمين

التعريف: المستقيمان المتعامدان، هما مستقيمان متقاطعان و يشكلان زاوية قائمة على الأقل.	الأولى إعدادي
طريقة 2: إذا كان مستقيمان متعامدان، فكل مستقيم موازي لأحدهما يكون عموديا على الآخر.	الأولى إعدادي
طريقة 3: إذا كان مستقيمان متوازيان فكل مستقيم عمودي على أحدهما يكون عموديا على الآخر.	الأولى إعدادي
طريقة 4: واسط قطعة هو مستقيم يمر من منتصفها و عمودي على حاملها.	الأولى إعدادي
طريقة 5: إذا كان ABCD معينا فإن: (BD) و (AC) متعامدان.	الأولى إعدادي
طريقة 6: إذا كان ABCD مستطيلا فإن: (AB) و (AD) متعامدان.	الأولى إعدادي
طريقة 7: إذا كان ABC مثلث متساوي الساقين في A ، و (D) منصف الزاوية [BÂC] أو واسط [BC] أو متوسط المثلث أو ارتفاعه المار من A فإن: المستقيم (D) عمودي على المستقيم (BC).	الأولى إعدادي
طريقة 8: (باستعمال مركز تعامد المثلث) في مثلث ABC . إذا كان (B'B) و (C'C) ارتفاعان لمثلث ABC متقاطعان في نقطة H . فإن النقطة H هي مركز تعامد المثلث ABC . و منه: المستقيم (AH) عمودي على المستقيم (BC).	الأولى إعدادي
طريقة 9 إذا كان المستقيم (D) مماس لـدائرة مركزها O في نقطة A . فإن المستقيمان (D) و (OA) متعامدان.	الأولى إعدادي
طريقة 10: إذا كان المثلث ABC محاط بدائرة قطرها [BC]. فإن المثلث ABC قائم الزاوية في النقطة A .	الثانية إعدادي
طريقة 11: ( مبرهنة فيتاغورس العكسية) في مثلث ABC ، إذا كانت: BC² = AB² + AC² فإن المثلث ABC قائم الزاوية في A.	الثالثة إعدادي
طريقة 12: إذا كانت : (d) معادلته y = mx + p و المستقيم ('d) معادلته y = ax + b . وa×m = -1 . فإن المستقيمان (d) و ('d) متعامدان.	الثالثة إعدادي

للبرهان على منتصف القطعة

طريقة 1: إذا كانت A و B وI نقط مستقيمية و IA = IB. فإن : النقطة I منتصف القطعة [AB]	الأولى إعدادي
طريقة 2: إذا كانت النقطة B مماثلة النقطة A بالنسبة لنقطة I فإن النقطة I منتصف القطعة [AB].	الأولى إعدادي
طريقة 3: إذا كانت I نقطة تقاطع قطري متوازي الأضلاع ABCD فإن: I منتصف [AC] و [BD].	الأولى إعدادي
طريقة 4: إذا كانت I الدائرة (C) و [AB] قطر للدائرة (C) فإن النقطة I منتصف القطعة [AB].	الأولى إعدادي
طريقة 5: إذا كانت I تقاطع واسط القطعة [AB] و المستقيم (AB) فإن I منتصف القطعة [AB].	الأولى إعدادي
طريقة 6: إذا كان ABC مثلث متساوي الساقين في A ، وH المسقط العمودي للنقطة A على المستقيم (BC), فإن: النقطة H منتصف القطعة [BC].	الأولى إعدادي
طريقة 7: (باستعمال مركز ثقل المثلث) في مثلث ABC . إذا كان (B'B) و (C'C) متوسطي لمثلث ABC متقاطعان في نقطة G. فإن النقطة G هي مركز ثقل المثلث ABC . و منه: المستقيم (AG) يمر من منتصف القطعة [BC].	الثانية إعدادي
طريقة 8: إذا كان ABC مثلث قائم الزاوية في A و كانت O مركز الدائرة المحيطة بالمثلث ABC. فإن النقطة O منتصف القطعة [BC].	الثانية إعدادي
طريقة 9: في مثلث ABC إذا كانت I منتصف [AB]، و النقطة J من المستقيم (AC)، و المستقيم (IJ) يوازي المستقيم (BC) فإن النقطة J منتصف القطعة [AC].	الثانية إعدادي
طريقة 10: إذا كانت: فإن النقطة Iمنتصف القطعة [AB].	الثانية إعدادي
طريقة 11:	الثالثة إعدادي

للبرهان على تقايس قطعتين

طريقة 1: إذا كانت M تنتمي إلى واسط القطعة [AB]. فإن: MA = MB.	الأولى إعدادي
طريقة 2: مماثلة قطعة بتماثل مركزي هي قطعة تقايسها.	الأولى إعدادي
طريقة 3: إذا كان ABC مثلث متساوي الساقين في A. فإن: AB = AC .	الأولى إعدادي
طريقة 4: إذا كان ABCD مستطيل. فإن: AC = BD.	الأولى إعدادي
طريقة 5: إذا كان ABCD معينا فإن: AB = BC = CD = DA.	الأولى إعدادي
طريقة 6: إذا كانت M نقطة من منصف الزاوية [xÔy] و النقطة H المسقط العمودي للنقطة M على المستقيم (Ox) و النقطة L المسقط العمودي للنقطة M على المستقيم (Oy) فإن: MH = ML.	الأولى إعدادي
طريقة 7: إذا كانت A و B تنتميان لنفس الدائرة التي مركزها O فإن: OA = OB.	الأولى إعدادي
طريقة 8: إذا كان ABCD متوازي أضلاع. فإن: AB = DC و AD = BC.	الأولى إعدادي
طريقة 9: إذا كان ABCD متوازي أضلاع مركزه O. فإن: OB = DO و AO = OC.	الأولى إعدادي
طريقة 10: إذا كان المثلث ABC قائم الزاوية في النقطة A ، و I منتصف [BC]. فإن : IA = IB = IC .	الثانية إعدادي
طريقة 11: ( مبرهنة فيتاغورس المباشرة) إذا كانت: المثلث ABC قائم الزاوية في A. فإنBC² = AB² + AC².	الثانية إعدادي
طريقة 12: مبرهنة طاليس المباشرة.	الثانية إعدادي
طريقة 13: العلاقات المترية و العلاقات المثلثية، في المثلث القائم الزاوية.	الثالثة إعدادي
طريقة 14: المثلثات المتقايسة و المثلثات المتشابهة.	الثالثة إعدادي

للبرهان أن رباعي متوازي الأضلاع

طريقة 1: إذا كانت كل ضلعان متقابلان في رباعي حاملاهما متوازيان فإن هذا الرباعي متوازي الأضلاع.	الأولى إعدادي
طريقة 2: في رباعي ABCD إذا كان لقطريه [AC] و [BD] نفس المنتصف فإن الرباعي ABCD متوازي الأضلاع.	الأولى إعدادي
طريقة 3: في رباعي محدب ABCD إذا كانت: AB = DC و AD = BC. فإن الرباعي ABCD متوازي الأضلاع.	الأولى إعدادي
طريقة 4: في رباعي محدب إذا كان ضلعان متقابلان متقايسان و حاملاهما متوازيان فإن هذا الرباعي متوازي الأضلاع.	الأولى إعدادي
طريقة 5: إذا كانت كل زاويتان متتاليتان في رباعي متكاملتان فإن هذا الرباعي متوازي الأضلاع.	الأولى إعدادي
طريقة 6: إذا كانت كل زاويتان متقابلتان في رباعي متقايستان فإن هذ الرباعي متوازي الأضلاع.	الأولى إعدادي
طريقة 7: إذا كانت النقط A و B و C مختلفة و غير مستقيمية و فإن الرباعي ABCD متوازي الأضلاع	الثانية و الثالثة إعدادي
طريقة 8: إذا كانت النقط A و B و C مختلفة و غير مستقيمية و فإن الرباعي ABCD متوازي الأضلاع	الثانية و الثالثة إعدادي
طريقة 9: إذا كانت النقط A و B و C مختلفة و غير مستقيمية و فإن الرباعي ABCD متوازي الأضلاع	الثالثة إعدادي

للبرهان أن مثلث قائم الزاوية

طريقة 1: المثلث القائم الزاوية هو مثلث له زاوية قائمة .	الأولى إعدادي
طريقة 2: في مثلث إذا كان مجموع زاويتين يساوي 90° فإن المثلث قائم الزاوية.	الأولى إعدادي
طريقة 3: إذا كان االرباعي ABCD مستطيلا فإن المثلث ABC قائم الزاوية في B.	الأولى إعدادي
طريقة 4: إذا كان الرباعي ABCD معينا مركزه O فإن المثلث OAB قائم الزاوية في O	الأولى إعدادي
طريقة 5: إذا كان المثلث ABC محاط بدائرة قطرها [BC] فإن المثلث ABC قائم الزاوية في A.	الثانية إعدادي
طريقة 6: ( مبرهنة فيتاغورس المباشرة ) في مثلث ABC ، إذا كان: BC² = AB² + AC² فإن المثلث ABC قائم الزاوية في A.	الثالثة إعدادي

عن موقع http://ad2math.com/12